IGNOU DYNAMIC SOLVER: MCA 5th sem /MCSE-003/Solved Assignment/Artificial Intelligence and Knowledge Management/2016-2017 New

Q.1.
A.1.

Heuristic Search

A heuristic is a method that

might not always find the best solution
but is guaranteed to find a good solution in reasonable time.

By sacrificing completeness it increases efficiency.
Useful in solving tough problems which
- could not be solved any other way.
- solutions take an infinite time or very long time to compute.

The classic example of heuristic search methods is the travelling salesman problem.
Heuristic Search methods Generate and Test Algorithm

generate a possible solution which can either be a point in the problem space or a path from the initial state.
test to see if this possible solution is a real solution by comparing the state reached with the set of goal states.
if it is a real solution, return. Otherwise repeat from 1.

This method is basically a depth first search as complete solutions must be created before testing. It is often called the British Museum method as it is like looking for an exhibit at random. A heuristic is needed to sharpen up the search. Consider the problem of four 6-sided cubes, and each side of the cube is painted in one of four colours. The four cubes are placed next to one another and the problem lies in arranging them so that the four available colours are displayed whichever way the 4 cubes are viewed. The problem can only be solved if there are at least four sides coloured in each colour and the number of options tested can be reduced using heuristics if the most popular colour is hidden by the adjacent cube.

Traveling salesman problem (TSP)
The traveling salesman problem (TSP) is to find the shortest hamiltonian cycle in a graph. This problem is NP-hard and thus interesting. There are a number of algorithms used to find optimal tours, but none are feasible for large instances since they all grow exponentially. We can get down to polynomial growth if we settle for near optimal tours. We gain speed, speed and speed at the cost of tour quality. So the interesting properties of heuristics for the TSP is mainly speed and closeness to optimal solutions. There are mainly two ways of finding the optimal length of a TSP instance. The first is to solve it optimally and thus finding the length. The other is to calculate the Held-Karp lower bound, which produces a lower bound to the optimal solution . This lower bound is the de facto standard when judging the performance of an approximation algorithm for the TSP.

Approximation
Solving the TSP optimally takes to long, instead one normally uses approximation algorithms, or heuristics. The difference is approximation algorithms give us a guarantee as to how bad solutions we can get. Normally specified as c times the optimal value. The algorithm guarantees a (1+1/c)- approximation for every c > 1. It is based om geometric partitioning and quad trees. Although theoretically c can be very large, it will have a negative effect on its running time (O(n(log2n) O(c) ) for two-dimensional problem instances).

3. Tour Construction
Tour construction algorithms have one thing in commmon, they stop when a solution is found and never tries to improve it. The best tour construction algorithms usually gets within 10-15% of optimality.

3.1. Nearest Neighbor
This is perhaps the simplest and most straightforward TSP heuristic. The key to this algorithm is to always visit the nearest city. Nearest Neighbor, O(n 2 ) 1. Select a random city. 2. Find the nearest unvisited city and go there. 3. Are there any unvisitied cities left? If yes, repeat step 2. 4. Return to the first city. The Nearest Neighbor algorithm will often keep its tours within 25% of the Held-Karp lower bound.

Even before mathematicians looked at this problem there were analytically minded salesmen and their employers who thought about it. Let us look at a very simple example. Suppose the diagram below shows the road distance between the three towns to which Hilda, who sells software to high schools, must travel (starting from home). The numbers near the line segments (edges) in the diagram are the driving distances between the locations.

Figure 1 (A 4-city TSP problem)

What we have above is a diagram consisting of dots and lines known as a graph. This is a special kind of graph known as a complete graph because each vertex is joined to every other one. Furthermore, we have assigned to each edge of the complete graph a weight, which could be a time, road distance, cost of a train or airplane ticket, etc. for the trip between the two locations at the endpoints of the edge. Usually these weights are taken as nonnegative numbers (but it is interesting to consider what interpretation might be put on using negative weights) which obey the triangle inequality. This means that given three locations X, Y, and Z the sum of the weights for any pair of the three edges the locations determine is at least as large as the weight on the third edge. (For a distance function, satisfying the triangle inequality is part of the usual definition, as is the requirement that the distance from A to B be the same as the distance from B to A.) In our example, we are assuming that we have a symmetric TSP - the cost in going from X to Y is the same as the cost in going from Y to X - but many interesting applications give rise to an asymmetric TSP in which the cost of going from X to Y may not be the same as the cost in going from Y to X.

The goal in solving a TSP is to find the minimum cost tour, the optimal tour. A tour of the vertices of a graph which visits each vertex (repeating no edge) once and only once is known as a Hamiltonian circuit. Thus, one can think of solving a TSP as finding a minimum cost Hamiltonian circuit in a complete graph with weights on the edges.

Q.2.
A.2.(i)Semantic Net:-

A semantic net (or semantic network) is a knowledge representation technique used for propositional information. So it is also called a propositional net. Semantic nets convey meaning. They are two dimensional representations of knowledge. Mathematically a semantic net can be defined as a labelled directed graph.
Semantic nets consist of nodes, links (edges) and link labels. In the semantic network diagram, nodes appear as circles or ellipses or rectangles to represent objects such as physical objects, concepts or situations. Links appear as arrows to express the relationships between objects, and link labels specify particular relations. Relationships provide the basic structure for organizing knowledge. The objects and relations involved need not be so concrete. As nodes are associated with other nodes semantic nets are also referred to as associative nets.

In the above figure all the objects are within ovals and connected using labelled arcs. Note that there is a link between Jill and FemalePersons with label MemberOf. Simlarly there is a MemberOf link between Jack and MalePersons and SisterOf link between Jill and Jack. The MemberOf link between Jill and FemalePersons indicates that Jill belongs to the category of female persons.

DISADVANTAGE OF SEMANTIC NETS

One of the drawbacks of semantic network is that the links between the objects represent only binary relations. For example, the sentence Run(ChennaiExpress, Chennai,Bangalore,Today) cannot be asserted directly.

There is no standard definition of link names.
ADVANTAGES OF SEMANTIC NETS

Semantic nets have the ability to represent default values for categories. In the above figure Jack has one leg while he is a person and all persons have two legs. So persons have two legs has only default status which can be overridden by a specific value.

They convey some meaning in a transparent manner.

They nets are simple and easy to understand.

They are easy to translate into PROLOG.

(ii) Rule Based Representation:-

Rules are the popular paradigm for representing knowledge. A rule based expert system is one whose knowledge base contains the domain knowledge coded in the form of rules.

ELEMENTS OF A RULE BASED EXPERT SYSTEM

A rule based expert system consists of the following components:

USER INTERFACE

This is a mechanism to support communication between and the system. The user interface may be a simple text-oriented display or a sophisticated, high resolution display. It is determined at the time of designing the system. Nowadays graphical user interfaces are very common for their user-friendliness.

EXPLANATION FACILITY
It explains the user about the reasoning process of the system. By keeping track of the rules that are fired, an explanation facility presents a chain of reasoning that led to a certain conclusion. So explanation facility is also called justifier. This feature makes a huge difference between expert systems and other conventional systems. almost all the commercial expert system shells do trace based explanation, that is, explaining the inferencing on a specific input data set. Some systems explain the knowledge base itself, and some explain the control strategy as well.

WORKING MEMORY

This is a database used to store collection of facts which will later be used by the rules. More effort may go into the design and implementation of the user interface than in the expert system knowledge base. Working memory is used by the inference engine to get facts and match them against the rules. The facts may be added to the working memory by applying some rules.

INFERENCE ENGINE

As the name implies the inference engine makes inferences. It decides which rules are satisfied by the facts, prioritizes them, and executes the rule with the highest priority. There are two types of inference: forward chaining and backward chaining. Forward chaining is reasoning from facts to the conclusion while backward chaining is from hypothesis to the facts that support this hypothesis. Whether an inference engine performs forward chining or backward chaining entirely depends on the design which in turn depends on the type of problem. Some of the systems that do forward chaining are OPS5 and CLIPS. EMYCIN one of the most popular systems performs backward chining. Some systems, ART and KEE, for example, offer both the techniques. Forward chaining is best suited for prognosis, monitoring and control. Backward chaining is generally used for diagnostic problems. Inference engine operates in cycles, executing a group of tasks until certain criteria causes that halt the execution. The taks to be done repeatedly are conflict resolution, act, match and check for halt. Multiple rules may be activated and put on the agenda during one cycle.

Q.3A.3.(a)

Comparison of Human Expert and Expert Systems

Time Availability : Human Expert (Working day). Expert Systems (any time)
Geographical : Human Expert (specific location). Expert Systems (wherever)
Security: Human Expert (not replaceable). Expert Systems (can be replaced)
Perishable : Human Expert (yes). Expert Systems (no)
Performance : Human Expert (variable). Expert Systems (consistent)
Speed:Human Expert (variable). Expert Systems (consistent and more fast)

The fundamental reason why the ES (Expert Systems) was developed to replace a experts:
Can provide expertise at all times and in various locations
Automatically doing routine tasks that require an expert.
An expert will retire or leave
An expert is expensive
Expertise is needed also in a hostile environment (hostile environtment)

Comparison of Conventional Systems and Expert System

Image result for conventional system vs expert system

A.3(ii)
(A)Travelling Salesman Problem (TSP):

Travelling Salesman Problem (TSP): Given a set of cities and distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point.
Note the difference between Hamiltonian Cycle and TSP. The Hamiltoninan cycle problem is to find if there exist a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle.

For example, consider the graph shown in figure on right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80.

The problem is a famous NP hard problem. There is no polynomial time know solution for this problem.

Following are different solutions for the traveling salesman problem.

Naive Solution:
1) Consider city 1 as the starting and ending point.
2) Generate all (n-1)! Permutations of cities.
3) Calculate cost of every permutation and keep track of minimum cost permutation.
4) Return the permutation with minimum cost.

Time Complexity: ?(n!)

Dynamic Programming:
Let the given set of vertices be {1, 2, 3, 4,….n}. Let us consider 1 as starting and ending point of output. For every other vertex i (other than 1), we find the minimum cost path with 1 as the starting point, i as the ending point and all vertices appearing exactly once. Let the cost of this path be cost(i), the cost of corresponding Cycle would be cost(i) + dist(i, 1) where dist(i, 1) is the distance from i to 1. Finally, we return the minimum of all [cost(i) + dist(i, 1)] values. This looks simple so far. Now the question is how to get cost(i)?
To calculate cost(i) using Dynamic Programming, we need to have some recursive relation in terms of sub-problems. Let us define a term C(S, i) be the cost of the minimum cost path visiting each vertex in set S exactly once, starting at 1 and ending at i.

(B)

WaterJugProblem

Statement :- We are given 2 jugs, a 4 liter one and a 3- liter one. Neither has any measuring markers on it. There is a pump that can be used to fill the jugs with water. How can we get exactly 2 liters of water in to the 4-liter jugs?

Solution:-

The state space for this problem can be defined as

{ ( i ,j ) i = 0,1,2,3,4 j = 0,1,2,3}

‘i’ represents the number of liters of water in the 4-liter jug and ‘j’ represents the number of liters of water in the 3-liter jug. The initial state is ( 0,0) that is no water on each jug. The goal state is to get ( 2,n) for any value of ‘n’.

To solve this we have to make some assumptions not mentioned in the problem. They are

1. We can fill a jug from the pump.

2. we can pour water out of a jug to the ground.

3. We can pour water from one jug to another.

4. There is no measuring device available.

The various operators (Production Rules) that are available to solve this problem may be stated as given in the following figure .

(C)Three missionaries and three cannibals find themselves on one side of a river. They have would like to get to the other side. But the missionaries are not sure what else the cannibals agreed to. So the missionaries managed the trip across the river in such a way that the number of missionaries on either side of the river is never less than the number of cannibals who are on the same side. The only boar available holds only two at a time. How can everyone get across the river without the missionaries risking being eaten?

Solution:-

The state for this problem can be defined as

{(i, j)/ i=0, 1, 2, 3, : j=0, 1, 2, 3}

where i represents the number missionaries in one side of a river . j represents the number of cannibals in the same side of river. The initial state is (3,3), that is three missionaries and three cannibals one side of a river , (Bank 1) and ( 0,0) on another side of the river (bank 2) . the goal state is to get (3,3) at bank 2 and (0,0) at bank 1.

To sole this problem we will make the following assumptions:

1. Number of cannibals should lesser than the missionaries on either side.

2. Only one boat is available to travel.

3. Only one or maximum of two people can go in the boat at a time.

4. All the six have to cross the river from bank.

5. There is no restriction on the number of trips that can be made to reach of the goal.

6. Both the missionaries and cannibals can row the boat.

This kind of problem is often solved by a graph search method. Represent the problem as a set of states which are snapshots of the world and operators which transform one state into another state are mapped to nodes of the graph and operators are the edges of the graph. The following procedure shows the graph search algorithm in PROLOG, for Missionaries and Cannibals Problem.

Path finding.

* Write a program to find path from one node to another.

* Must avoid cycles

* A template for the clause is

path(start, Finish, Visited, Path).
Start - the name of the starting node.
Finish - the name of the finishing node.
Visited - the list of nodes aready visited.
Path - the list of nodes on the path, including Start and Finish.

Program for finding a Path.

* The search for a path terminates when we have nowhere t0o go.

path {Node, Node,.., [Node]}

A path from start to Finish, starts with a node, X,connected to start followed by a path from X to Finish.

path (Start, Finish, Visited, {Start [ Path]} :-
edge (Start,X),
not (member( X,Visited)),
path(x,Finish, {X [vISITED],Path)
member (X,[X I_ I).
member (X,I_ IYI):- member(X,Y).

Representing the state.

Now we returen to the peoblem or rrepresenting tyhe missionaries and cannibals problem;
*A State is one "snapshot" in time.

*For this problem the only infoemation we need to fully characterize the state is :
*the number of missionaries on the left bank,
*the number of cannibals on the left bank,
*the side the boat is on.

All other information can be deduced from these thres items.

In PROLOG, the state can be representted by a 3-arity term, state (Missionaries,Cannibals, State).

Three missionaries and three cannibals find themselves on one side of a river. They have would like to get to the other side. But the missionaries are not sure what else the cannibals agreed to. So the missionaries managed the trip across the river in such a way that the number of missionaries on either side of the river is never less than the number of cannibals who are on the same side. The only boar available holds only two at a time. How can everyone get across the river without the missionaries risking being eaten?

Solution:-

The state for this problem can be defined as

{(i, j)/ i=0, 1, 2, 3, : j=0, 1, 2, 3}

To sole this problem we will make the following assumptions:

1. Number of cannibals should lesser than the missionaries on either side.

2. Only one boat is available to travel.

3. Only one or maximum of two people can go in the boat at a time.

4. All the six have to cross the river from bank.

5. There is no restriction on the number of trips that can be made to reach of the goal.

6. Both the missionaries and cannibals can row the boat.

Q.4.
A.4.(a)

Factorial Revisited

To better understand how auxiliary functions and accumulator variables are used, let us revisit the problem of computing factorials. The following is an alternative implementation of the factorial function:

(defun fast-factorial (N)
  "A tail-recursive version of factorial."
  (fast-factorial-aux N 1))

(defun fast-factorial-aux (N A)
  "Multiply A by the factorial of N."
  (if (= N 1)
      A
    (fast-factorial-aux (- N 1) (* N A))))

Let us defer the explanation of why the function is named "fast-factorial", and treat it as just another way to implement factorial. Notice the structural similarity between this pair of functions and those for computing list reversal. The auxiliary function (fast-factorial-aux N A) computes the product of A and the N'th factorial. The driver function computes N! by calling fast-factorial-aux with A set to 1. Now, the correctness of the auxiliary function (i.e. that (fast-factorial-aux N A) indeed returns the product of N! and A) can be established as follows. N is either one or larger than one.

Case 1: N = 1
The product of A and 1! is simply A * 1! = A.
Case 2: N > 1
Since N! = N * (N-1)!, we then have N! * A = (N-1)! * (N * A), thus justifying our implementation.

Tracing both fast-factorial and fast-factorial-aux, we get the following:

USER(3): (trace fast-factorial fast-factorial-aux)  
(FAST-FACTORIAL-AUX FAST-FACTORIAL)
USER(4): (fast-factorial 4)
 0: (FAST-FACTORIAL 4)
   1: (FAST-FACTORIAL-AUX 4 1)
     2: (FAST-FACTORIAL-AUX 3 4)
       3: (FAST-FACTORIAL-AUX 2 12)
         4: (FAST-FACTORIAL-AUX 1 24)
         4: returned 24
       3: returned 24
     2: returned 24
   1: returned 24
 0: returned 24
24

If we compare the structure of fast-factorial with list-reverse, we notice certain patterns underlying the use of accumulator variables in auxiliary functions:

An auxiliary function generalizes the functionality of the driver function by promising to compute the function of interest and also combine the result with the value of the accumulator variable. In the case of list-reverse-aux, our original interest were computing list reversals, but then the auxiliary function computes a more general concept, namely, that of appending an auxiliary list to some list reversal. In the case of fast-factorial-aux, our original interest were computing factorials, but the auxiliary function computes a more general value, namely, the product of some auxiliary number with a factorial.
At each level of recursion, the auxiliary function reduces the problem into a smaller subproblem, and accumulating intermediate results in the accumulator variable. In the case of list-reverse-aux, recursion is applied to the sublist (rest L), while (first L) is cons'ed with A. In the case of fast-factorial, recursion is applied to (N - 1)!, while N is multiplied with A.
The driver function initiates the recursion by providing an initial value for the auxiliary variable. In the case of computing list reversals, list-reverse initializes A to nil. In the case of computing factorials, fast-factorial initializes A to 1.

Now that you understand how fast-factorial works, we explain where the adjective "fast" come from ...

Tail Recursions

Recursive functions are usually easier to reason about. Notice how we articulate the correctness of recursive functions in this and the previous tutorial. However, some naive programmers complain that recursive functions are slow when compared to their iterative counter parts. For example, consider the original implementation of factorial we saw in the previous tutorial:

(defun factorial (N)
  "Compute the factorial of N."
  (if (= N 1)
      1
    (* N (factorial (- N 1)))))

It is fair to point out that, as recursion unfolds, stack frames will have to be set up, function arguments will have to be pushed into the stack, so on and so forth, resulting in unnecessary runtime overhead not experienced by the iterative counterpart of the above factorial function:

int factorial(int N) {
  int A = 1;
  while (N != 1) {
    A = A * N;
    N = N - 1;
  }
  return A;
}

Because of this and other excuses, programmers conclude that they could write off recursive implementations ...Modern compilers for functional programming languages usually implement tail-recursive call optimizations which automatically translate a certain kind of linear recursion into efficient iterations. A linear recursive function is tail-recursive if the result of each recursive call is returned right away as the value of the function. Let's examine the implementation of fast-factorial again:

(defun fast-factorial (N)
  "A tail-recursive version of factorial."
  (fast-factorial-aux N 1))

(defun fast-factorial-aux (N A)
  "Multiply A by the factorial of N."
  (if (= N 1)
      A
    (fast-factorial-aux (- N 1) (* N A))))

Notice that, in fast-factorial-aux, there is no work left to be done after the recursive call (fast-factorial-aux (- N 1) (* N A)). Consequently, the compiler will not create new stack frame or push arguments, but instead simply bind (- N 1) to N and (* N A) to A, and jump to the beginning of the function. Such optimization effectively renders fast-factorial as efficient as its iterative counterpart. Notice also the striking structural similarity between the two.

(B) PROLOG

%trace

predicates

father(symbol,symbol)

mother(symbol,symbol)

male(symbol)

female(symbol)

sister(symbol,symbol)

brother(symbol,symbol)

uncle(symbol,symbol)

wife(symbol,symbol)

aunty(symbol,symbol)

bhabhi(symbol,symbol)

cousin(symbol,symbol)

nephew(symbol,symbol)

grand_son(symbol,symbol)

grand_duaghter(symbol,symbol)

clauses

sister(X,Y) :- father(X,A),father(Y,A),female(Y).

father(dhanjiBhai,vithhaldas).

father(chuniBhai,vithhaldas).

father(harshad,dhanjibhai).

father(darshan,dhanjibhai).

father(nilam,dhanjibhai).

father(kiran,dhanjibhai).

father(kamleshbhai,chunibhai).

mother(harshad,prabhaben).

mother(X,Y) :- father(X,Z),wife(Y,Z)

brother(X,Y) :- father(X,A),father(Y,A),male(X).

% brother(X,Y) :- brother(Y,X).

male(harshad).

male(darshan).

male(dhanjibhai).

male(chunibhai).

female(nilam).

female(kiran).

female(prabhaben).

female(nimishaben).

female(kokilaben).

wife(prabhaben,dhanjibhai).

wife(nimishaben,kamleshbhai).

Wife(kokilaben,chunibhai).

grand_son(X,Y) :- father(A,Y),father(X,A),male(X).

grand_duaghter(X,Y) :- father(A,Y),father(X,A),female(Y).

uncle(X,Y) :- father(X,Z),brother(Y,Z).

aunty(X,Y) :- wife(Y,Z),

brother(Z,W),

father(X,W).

bhabhi(X,Y) :- wife(X,Z),cousin(Y,Z),female(X)

cousin(X,Y) :- father(X,A),father(Y,B),brother(A,B).

nephew(X,Y) :- wife(Y,A),brother(A,B),father(X,B),male(X).

Q.5.

A.5.

An AI system is composed of an agent and its environment. The agents act in their environment. The environment may contain other agents.

What are Agent and Environment?

An agent is anything that can perceive its environment through sensors and acts upon that environment through effectors.

A human agent has sensory organs such as eyes, ears, nose, tongue and skin parallel to the sensors, and other organs such as hands, legs, mouth, for effectors.
A robotic agent replaces cameras and infrared range finders for the sensors, and various motors and actuators for effectors.
A software agent has encoded bit strings as its programs and actions.

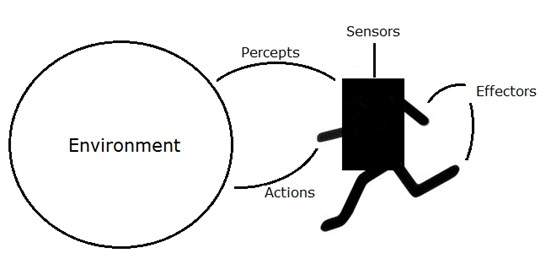
Agent Terminology

Performance Measure of Agent − It is the criteria, which determines how successful an agent is.
Behavior of Agent − It is the action that agent performs after any given sequence of percepts.
Percept − It is agent’s perceptual inputs at a given instance.
Percept Sequence − It is the history of all that an agent has perceived till date.
Agent Function − It is a map from the precept sequence to an action.

Rationality

Rationality is nothing but status of being reasonable, sensible, and having good sense of judgment.

Rationality is concerned with expected actions and results depending upon what the agent has perceived. Performing actions with the aim of obtaining useful information is an important part of rationality.

What is Ideal Rational Agent?

An ideal rational agent is the one, which is capable of doing expected actions to maximize its performance measure, on the basis of −

Its percept sequence
Its built-in knowledge base

Rationality of an agent depends on the following four factors −

The performance measures, which determine the degree of success.
Agent’s Percept Sequence till now.
The agent’s prior knowledge about the environment.
The actions that the agent can carry out.

A rational agent always performs right action, where the right action means the action that causes the agent to be most successful in the given percept sequence. The problem the agent solves is characterized by Performance Measure, Environment, Actuators, and Sensors (PEAS).

The Structure of Intelligent Agents

Agent’s structure can be viewed as −

Agent = Architecture + Agent Program
Architecture = the machinery that an agent executes on.
Agent Program = an implementation of an agent function.

Simple Reflex Agents

They choose actions only based on the current percept.
They are rational only if a correct decision is made only on the basis of current precept.
Their environment is completely observable.

Condition-Action Rule − It is a rule that maps a state (condition) to an action.

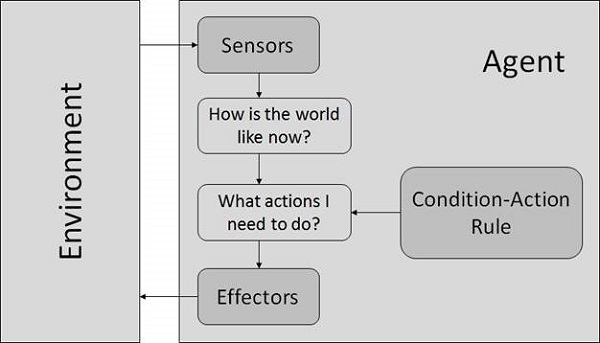
Model Based Reflex Agents

They use a model of the world to choose their actions. They maintain an internal state.

Model − The knowledge about how the things happen in the world.

Internal State − It is a representation of unobserved aspects of current state depending on percept history.

Updating the state requires the information about −

How the world evolves.
How the agent’s actions affect the world.

Goal Based Agents

They choose their actions in order to achieve goals. Goal-based approach is more flexible than reflex agent since the knowledge supporting a decision is explicitly modeled, thereby allowing for modifications.

Goal − It is the description of desirable situations.

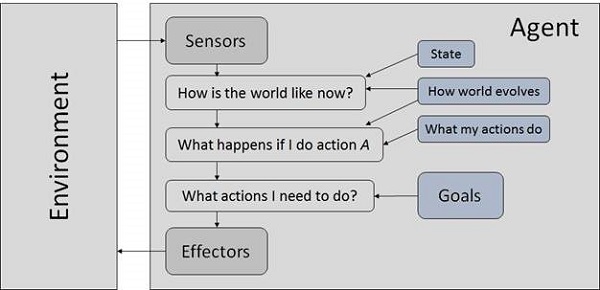
Utility Based Agents

They choose actions based on a preference (utility) for each state. Goals are inadequate when −

There are conflicting goals, out of which only few can be achieved.
Goals have some uncertainty of being achieved and you need to weigh likelihood of success against the importance of a goal.

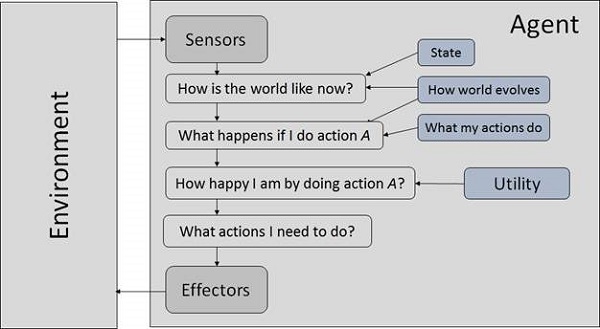
Nature of Environments

Some programs operate in the entirely artificial environment confined to keyboard input, database, computer file systems and character output on a screen.

In contrast, some software agents (software robots or softbots) exist in rich, unlimited softbots domains. The simulator has a very detailed, complex environment. The software agent needs to choose from a long array of actions in real time. A softbot designed to scan the online preferences of the customer and show interesting items to the customer works in the real as well as an artificial environment.

The most famous artificial environment is the Turing Test environment, in which one real and other artificial agents are tested on equal ground. This is a very challenging environment as it is highly difficult for a software agent to perform as well as a human.

Turing Test

The success of an intelligent behavior of a system can be measured with Turing Test.

Two persons and a machine to be evaluated participate in the test. Out of the two persons, one plays the role of the tester. Each of them sits in different rooms. The tester is unaware of who is machine and who is a human. He interrogates the questions by typing and sending them to both intelligences, to which he receives typed responses.

This test aims at fooling the tester. If the tester fails to determine machine’s response from the human response, then the machine is said to be intelligent.

Properties of Environment

The environment has multifold properties −

Discrete / Continuous − If there are a limited number of distinct, clearly defined, states of the environment, the environment is discrete (For example, chess); otherwise it is continuous (For example, driving).
Observable / Partially Observable − If it is possible to determine the complete state of the environment at each time point from the percepts it is observable; otherwise it is only partially observable.
Static / Dynamic − If the environment does not change while an agent is acting, then it is static; otherwise it is dynamic.
Single agent / Multiple agents − The environment may contain other agents which may be of the same or different kind as that of the agent.
Accessible / Inaccessible − If the agent’s sensory apparatus can have access to the complete state of the environment, then the environment is accessible to that agent.
Deterministic / Non-deterministic − If the next state of the environment is completely determined by the current state and the actions of the agent, then the environment is deterministic; otherwise it is non-deterministic.
Episodic / Non-episodic − In an episodic environment, each episode consists of the agent perceiving and then acting. The quality of its action depends just on the episode itself. Subsequent episodes do not depend on the actions in the previous episodes. Episodic environments are much simpler because the agent does not need to think ahead.
Q.6.

A.6.(a)
A.6.(b)
The physical attributes of a person can be represented as in Fig. 9.

A Semantic Network

These values can also be represented in logic as: isa(person, mammal), instance(Mike-Hall, person) team(Mike-Hall, Cardiff)

We have already seen how conventional predicates such as lecturer(dave) can be written as instance (dave, lecturer) Recall that isa and instance represent inheritance and are popular in many knowledge representation schemes. But we have a problem: How we can have more than 2 place predicates in semantic nets? E.g. score(Cardiff, Llanelli, 23-6) Solution:
- Create new nodes to represent new objects either contained or alluded to in the knowledge, game and fixture in the current example.
- Relate information to nodes and fill up slots (Fig: 10).
Fig. A Semantic Network for n-Place Predicate
As a more complex example consider the sentence: John gave Mary the book. Here we have several aspects of an event.
Q.7.
A.7.(a)

A.7.(b)

(i) Learning:-
The following components are part of any learning problem:

task

The behavior or task that is being improved

data

The experiences that are used to improve performance in the task

measure of improvement

How the improvement is measured - for example, new skills that were not present initially, increasing accuracy in prediction, or improved speed

Consider the agent internals of. The problem of learning is to take in prior knowledge and data (e.g., about the experiences of the agent) and to create an internal representation (the knowledge base) that is used by the agent as it acts. This internal representation could be the raw experiences themselves, but it is typically a compact representation that summarizes the data. The problem of inferring an internal representation based on examples is often called induction and can be contrasted with deduction, which is deriving consequences of a knowledge base, and abduction, which is hypothesizing what may be true about a particular case.

There are two principles that are at odds in choosing a representation scheme:

The richer the representation scheme, the more useful it is for subsequent problems solving. For an agent to learn a way to solve a problem, the representation must be rich enough to express a way to solve the problem.

The richer the representation, the more difficult it is to learn. A very rich representation is difficult to learn because it requires a great deal of data, and often many different hypotheses are consistent with the data.

The representations required for intelligence are a compromise between many desiderata . The ability to learn the representation is one of them, but it is not the only one.

Learning techniques face the following issues:

Task

Virtually any task for which an agent can get data or experiences can be learned. The most commonly studied learning task is supervised learning: given some input features, some target features, and a set of training examples where the input features and the target features are specified, predict the target features of a new example for which the input features are given. This is called classification when the target variables are discrete and regression when the target features are continuous.

Other learning tasks include learning classifications when the examples are not already classified (unsupervised learning), learning what to do based on rewards and punishments (reinforcement learning), learning to reason faster (analytic learning), and learning richer representations such as logic programs (inductive logic programming) or Bayesian networks.

Feedback

Learning tasks can be characterized by the feedback given to the learner. In supervised learning, what has to be learned is specified for each example. Supervised classification occurs when a trainer provides the classification for each example. Supervised learning of actions occurs when the agent is given immediate feedback about the value of each action. Unsupervised learning occurs when no classifications are given and the learner must discover categories and regularities in the data. Feedback often falls between these extremes, such as in reinforcement learning, where the feedback in terms of rewards and punishments occurs after a sequence of actions. This leads to the credit-assignment problem ofdetermining which actions were responsible for the rewards or punishments. For example, a user could give rewards to the delivery robot without telling it exactly what it is being rewarded for. The robot then must either learn what it is being rewarded for or learn which actions are preferred in which situations. It is possible that it can learn what actions to perform without actually determining which consequences of the actions are responsible for rewards.

Representation

For an agent to use its experiences, the experiences must affect the agent's internal representation. Much of machine learning is studied in the context of particular representations (e.g., decision trees, neural networks, or case bases). This chapter presents some standard representations to show the common features behind learning.

Online and offline

In offline learning, all of the training examples are available to an agent before it needs to act. In online learning, training examples arrive as the agent is acting. An agent that learns online requires some representation of its previously seen examples before it has seen all of its examples. As new examples are observed, the agent must update its representation. Typically, an agent never sees all of its examples. Active learning is a form of online learning in which the agent acts to acquire useful examples from which to learn. In active learning, the agent reasons about which examples would be useful to learn from and acts to collect these examples.

Measuring success

Learning is defined in terms of improving performance based on some measure. To know whether an agent has learned, we must define a measure of success. The measure is usually not how well the agent performs on the training experiences, but how well the agent performs for new experiences.

(ii) Understanding

Natural Language Processing (NLP) refers to AI method of communicating with an intelligent systems using a natural language such as English.

Processing of Natural Language is required when you want an intelligent system like robot to perform as per your instructions, when you want to hear decision from a dialogue based clinical expert system, etc.

The field of NLP involves making computers to perform useful tasks with the natural languages humans use. The input and output of an NLP system can be −

Speech

Written Text

Components of NLP

There are two components of NLP as given −

Natural Language Understanding (NLU)

Understanding involves the following tasks −

Mapping the given input in natural language into useful representations.

Analyzing different aspects of the language.

Natural Language Generation (NLG)

It is the process of producing meaningful phrases and sentences in the form of natural language from some internal representation.

It involves −

Text planning − It includes retrieving the relevant content from knowledge base.

Sentence planning − It includes choosing required words, forming meaningful phrases, setting tone of the sentence.

Text Realization − It is mapping sentence plan into sentence structure.

The NLU is harder than NLG.

Difficulties in NLU

NL has an extremely rich form and structure.

It is very ambiguous. There can be different levels of ambiguity −

Lexical ambiguity − It is at very primitive level such as word-level.

For example, treating the word “board” as noun or verb?

Syntax Level ambiguity − A sentence can be parsed in different ways.

For example, “He lifted the beetle with red cap.” − Did he use cap to lift the beetle or he lifted a beetle that had red cap?

Referential ambiguity − Referring to something using pronouns. For example, Rima went to Gauri. She said, “I am tired.” − Exactly who is tired?

One input can mean different meanings.

Many inputs can mean the same thing.

(iii) The Turing Test

The Turing Test
Alan Turing and the Imitation Game

Natural Language Processing (NLP)
   Partly out of an attempt to pass Turing's test, and partly just for the fun of it, there arose, largely in the 1970s, a group of programs that tried to cross the first human-computer barrier: language. These programs, often fairly simple in design, employed small databases of (usually English) language combined with a series of rules for forming intelligent sentences. While most were woefully inadequate, some grew to tremendous popularity. Perhaps the most famous such program was Joseph Weizenbaum's ELIZA. Written in 1966 it was one of the first and remained for quite a while one of the most convincing. ELIZA simulates a Rogerian psychotherapist (the Rogerian therapist is empathic, but passive, asking leading questions, but doing very little talking. e.g. "Tell me more about that," or "How does that make you feel?") and does so quite convincingly, for a while. There is no hint of intelligence in ELIZA's code, it simply scans for keywords like "Mother" or "Depressed" and then asks suitable questions from a large database. Failing that, it generates something generic in an attempt to elicit further conversation. Most programs since have relied on similar principles of keyword matching, paired with basic knowledge of sentence structure. There is however, no better way to see what they are capable of than to try them yourself. We have compiled a set of links to some of the more famous attempts at NLP. Students are encouraged to interact with these programs in order to get a feeling for their strengths and weaknesses, but many of the pages provided here link to dozens of such programs, don't get lost among the artificial people.

   Alan Turing, in a 1951 paper, proposed a test called "The Imitation Game" that might finally settle the issue of machine intelligence. The first version of the game he explained involved no computer intelligence whatsoever. Imagine three rooms, each connected via computer screen and keyboard to the others. In one room sits a man, in the second a woman, and in the third sits a person - call him or her the "judge". The judge's job is to decide which of the two people talking to him through the computer is the man. The man will attempt to help the judge, offering whatever evidence he can (the computer terminals are used so that physical clues cannot be used) to prove his man-hood. The woman's job is to trick the judge, so she will attempt to deceive him, and counteract her opponent's claims, in hopes that the judge will erroneously identify her as the male.
   What does any of this have to do with machine intelligence? Turing then proposed a modification of the game, in which instead of a man and a woman as contestants, there was a human, of either gender, and a computer at the other terminal. Now the judge's job is to decide which of the contestants is human, and which the machine. Turing proposed that if, under these conditions, a judge were less than 50% accurate, that is, if a judge is as likely to pick either human or computer, then the computer must be a passable simulation of a human being and hence, intelligent. The game has been recently modified so that there is only one contestant, and the judge's job is not to choose between two contestants, but simply to decide whether the single contestant is human or machine.
   The dictionary.com entry on the Turing Test is short, but very clearly stated. A longer, but point-form review of the imitation game and its modifications written by Larry Hauser,  (if link fails, for a local copy) is also available. Hauser's page may not contain enough detail to explain the test, but it is an excellent reference or study guide and contains some helpful diagrams for understanding the interplay of contestant and judge. The page also makes reference to John Searle's Chinese Room, a thought experiment developed as an attack on the Turing test and similar "behavioural" intelligence tests. We will discuss the Chinese Room in the next section.

(iv)Uncertainity

Let action At = leave for airport t minutes before flight Will At get me there on time? Problems:

1. partial observability (road state, other drivers' plans, etc.)

2. noisy sensors (traffic reports)

3. uncertainty in action outcomes (flat tire, etc.)

4. immense complexity of modeling and predicting traffic Hence a purely logical approach either 1. risks falsehood: “A25 will get me there on time”, or 2. leads to conclusions that are too weak for decision making: “A2

5 will get me there on time if there's no accident on the bridge and it doesn't rain and my tires remain intact etc etc.” (A1440 might reasonably be said to get me there on time but I'd have to stay overnight in the airport …)

Methods for handling uncertainty

• Default or nonmonotonic logic: – Assume my car does not have a flat tire – Assume A25 works unless contradicted by evidence
• Issues: What assumptions are reasonable? How to handle contradiction?
• Rules with fudge factors: – A25 |→0.3 get there on time – Sprinkler |→ 0.99 WetGrass – WetGrass |→ 0.7 Rain
• Issues: Problems with combination, e.g., Sprinkler causes Rain??
• Probability – Model agent's degree of belief – Given the available evidence, – A25 will get me there on time with probability 0.04

(v)AI Problems

AI is developing with such an incredible speed, sometimes it seems magical. There is an opinion among researchers and developers that AI could grow so immensely strong that it would be difficult for humans to control.

Humans developed AI systems by introducing into them every possible intelligence they could, for which the humans themselves now seem threatened.

Threat to Privacy

An AI program that recognizes speech and understands natural language is theoretically capable of understanding each conversation on e-mails and telephones.

Threat to Human Dignity

AI systems have already started replacing the human beings in few industries. It should not replace people in the sectors where they are holding dignified positions which are pertaining to ethics such as nursing, surgeon, judge, police officer, etc.

Threat to Safety

The self-improving AI systems can become so mighty than humans that could be very difficult to stop from achieving their goals, which may lead to unintended consequences.

Q.8.
A.8.

When a problem can be divided into a set of sub problems, where each sub problem can be solved separately and a combination of these will be a solution, AND-OR graphs or AND - OR trees are used for representing the solution. The decomposition of the problem or problem reduction generates AND arcs. One AND are may point to any number of successor nodes. All these must be solved so that the arc will rise to many arcs, indicating several possible solutions. Hence the graph is known as AND - OR instead of AND. Figure shows an AND - OR graph.

An algorithm to find a solution in an AND - OR graph must handle AND area appropriately. A* algorithm can not search AND - OR graphs efficiently. This can be understand from the give figure.

FIGURE : AND - OR graph

In figure (a) the top node A has been expanded producing two area one leading to B and leading to C-D . the numbers at each node represent the value of f ' at that node (cost of getting to the goal state from current state). For simplicity, it is assumed that every operation(i.e. applying a rule) has unit cost, i.e., each are with single successor will have a cost of 1 and each of its components. With the available information till now , it appears that C is the most promising node to expand since its f ' = 3 , the lowest but going through B would be better since to use C we must also use D' and the cost would be 9(3+4+1+1). Through B it would be 6(5+1).

Thus the choice of the next node to expand depends not only n a value but also on whether that node is part of the current best path form the initial mode. Figure (b) makes this clearer. In figure the node G appears to be the most promising node, with the least f ' value. But G is not on the current beat path, since to use G we must use GH with a cost of 9 and again this demands that arcs be used (with a cost of 27). The path from A through B, E-F is better with a total cost of (17+1=18). Thus we can see that to search an AND-OR graph, the following three things must be done.

1. traverse the graph starting at the initial node and following the current best path, and accumulate the set of nodes that are on the path and have not yet been expanded.

2. Pick one of these unexpanded nodes and expand it. Add its successors to the graph and computer f ' (cost of the remaining distance) for each of them.

3. Change the f ' estimate of the newly expanded node to reflect the new information produced by its successors. Propagate this change backward through the graph. Decide which of the current best path.

The propagation of revised cost estimation backward is in the tree is not necessary in A* algorithm. This is because in AO* algorithm expanded nodes are re-examined so that the current best path can be selected. The working of AO* algorithm is illustrated in figure as follows:

Saturday, 1 April 2017

MCA 5th sem /MCSE-003/Solved Assignment/Artificial Intelligence and Knowledge Management/2016-2017 New﻿

Q.1.A.1.